Skip to main content

5.9.2 Negative Binomial

The command used to run a Negative Binomial analysis is `negative-binomial'.

The first variable in the list is the dependent variable (counting variable that counts occurrences of a given event). Other variables (explanatory variables) can be specified in the same way as with OLS (cf. the `regress' command).

Available options:

  • noconstant: Suppresses the constant term

  • level(): Change from default 95% confidence interval

  • robust: Robust standard errors

  • cluster(): Use cluster variable (cannot be used together with robust)

  • control(): Do not show coefficient estimates for selected variables

  • irr: Reports incidence rate ratio values ​​instead of coefficient values ​​(the values ​​are transformed through the natural exponential function). The value 1 means no effect. Values ​​above 1 mean a positive effect, while values ​​below 1 mean a negative effect.

  • exposure(): Includes exposure variable (categorical variable). This represents the "amount" of exposure to the process generating counts. The variable entered inside the parentheses must be categorical and must not contain 0 values. For example, if you model the number of car accidents in different cities, attachment to city can be an exposure variable. The exposure variable is automatically log-transformed (natural logarithm) and included as an offset in the model, meaning it will adjust the count response for the amount of exposure. The other estimates are then corrected based on this variable, so that they become more correct. Note that the `exposure' variable should not be entered as an explanatory variable in the model.

Factor variables, and cluster and robust estimation can also be used. The procedure is the same as for ordinary linear regression. See respectively chapter 5.4.1 and 5.4.3 for more information on this. For a full list of possibilities, use the help negative-binomial command.

Example of Negative Binomial Regression:

IMPORTANT

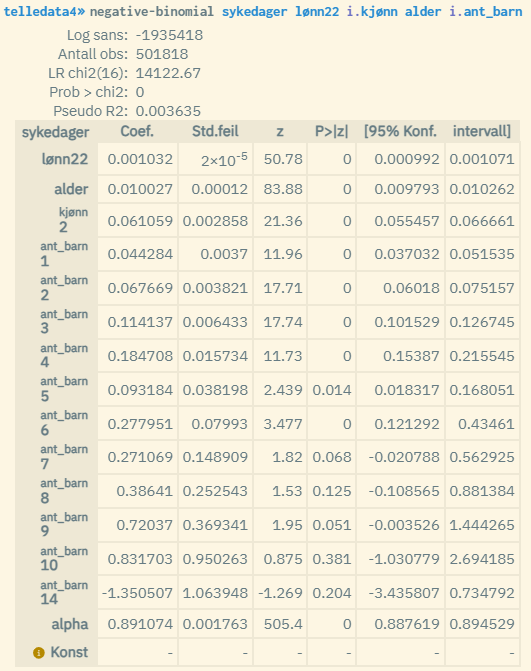
Note that the implementation of the counter regression Negative Binomial in microdata.no is not compatible with statistical models where at least one of the explanatory variables has too high a value (this will typically apply to income variables). It is recommended to transform the values ​​of the relevant variables so that they fall below a limit value of approx. 400 (this can be done by dividing by a factor or using e.g. a logarithm transformation). If this is not done, you risk getting a result that only shows empty values. However, as long as estimates are reported for all the explanatory variables, you do not need to perform any transformation.

Negative Binomial vs. Poisson​

The difference between a Poisson regression and a Negative Binomial regression is that in the latter the parameter alpha is included to capture extra variance (overdispersion), and the value of this is reported at the bottom of the list of coefficient estimates (above the constant term). The parameter is thus used to scale the variance of the model1.

An alpha value of 0 means that the model is identical to a Poisson model where variance = mean for the response variable, and that a Poisson regression is more appropriate to use. Positive alpha values ​​indicate overdispersion (greater spread), and the higher the value, the greater the spread. In the example above, the value is 0.89. This suggests that there is a relatively large degree of overdispersion and that Negative Binomial regression is possibly best to use (although Pseudo R2 has a lower value compared to Poisson).

Source:

The algorithms for the negative-binomial command are based on the function NegativeBinomial found in the Statsmodels module in Python.


Footnote:

Footnotes​

  1. The variance of a Negative Binomial model can be expressed as follows: Variance = μ + α * μ2 , where μ = average of Y, α = alpha. In a Poisson model, alpha is equal to 0 so that variance = mean. ↩